We try to understand the connections between history, genetic diversity, biology, and disease. We do this through creative math and collaborations with international consortia. Recently, we have been working on reconstructing histories of populations with very diverse genetic heritage, including Hispanic/Latinos and African-Americans, and found that some nifty math tricks enabled us to track the impact of historical events very accurately. We are also interested in using math tools to improve our understanding of fundamental properties of human biology, such as the rates of mutation and selection.

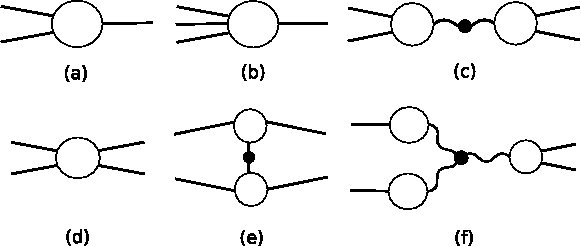
I studied the effect of very high pressures on the structure of solids, with N.W. Ashcroft. The main tools used in this project were electronic density functional theory (DFT) and nonlinear perturbation theory, and I became interested, more generally, in the structure of perturbation approaches to DFT. This led to the discovery of an interesting diagrammatic identity that can be used to obtain relevant high-order corrections to low-order perturbation calculations in metallic systems, but also in classical systems such as colloidal suspensions.

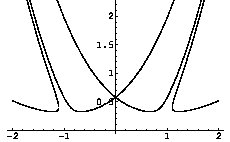
As a Master's student with Pavel Winternitz, I studied dynamical systems, particularly the relationship between the analytical solvability (or integrability) of dynamical systems and their behavior, with an emphasis on superintegrable Hamiltonians, that is, Hamiltonians with more invariants than degrees of freedom. I discovered many new superintegrable Hamiltonians, and found interesting relationships between their quantum and classical counterparts.